La radiochronologie

Certaines roches peuvent être datées grâce à la radioactivité. Ces procédés sont complexes mais à présent bien maîtrisés. Je ne parlerai pas de la datation au carbone 14, qui est la plus connue mais qui ne peut être appliquée qu’à des restes d’organismes vivants vieux de moins de 50 000 ans. Cela relève plus du domaine de l’archéologie que de la géologie.

Tout repose sur la désintégration radioactive de certains noyaux atomiques. Lors de la radioactivité alpha, deux protons et deux neutrons, constituant un noyau d’hélium, sont éjectés. Lors de la radioactivité bêta, un neutron se transforme en un proton en émettant un électron et un antineutrino électronique. Ces évènements sont dictés par la nature des particules élémentaires et de leurs interactions. Comme ils sont totalement aléatoires, il est impossible de dire quand un noyau va se désintégrer. Néanmoins, les évènements aléatoires obéissent à des lois. Avec la radioactivité, la probabilité qu’un noyau se désintègre ne dépend pas du temps. À partir de là, on peut calculer le nombre de noyaux au temps t, P(t), en fonction du nombre de noyaux au temps 0, P(0). La décroissance est exponentielle : aux temps T, 2T, 3T, … , ce nombre est divisé par 2, puis encore par 2, puis encore par 2, et ainsi de suite. Ce nombre T est la demi-vie de l’élément considéré.

Cela s’écrit :

P(t) = P(0) exp (‒ λt).

Le nombre λ, appelé la constante de désintégration, est égale à ln 2 / T.

Le noyau, qualifié de « père », se transforme en un autre noyau, qualifié de « fils ». On note F(t) le nombre de noyaux fils au temps t. Évidemment, le nombre de noyaux fils apparus au temps t est égal au nombre de noyaux pères disparus :

F(t) ‒ F(0) = P(0) ‒ P(t).

Cela donne la relation très importante :

F(t) = F(0) + P(t) [exp (λt) ‒ 1].

Le géochimiste peut mesurer la teneur en noyaux (ou atomes, ou éléments) pères et fils d’une roche, ou plutôt d’un minéral. Ce qu’il veut connaître, c’est son âge. Il s’agit de la quantité que j’ai appelée t. Cette formule lui permet de calculer t, à condition qu’il connaisse également la quantité d’atomes fils F(0) lors de la formation de la roche, or elle est généralement inconnue.

Il y a une autre difficulté, c’est qu’il doit supposer que pendant tout ce temps, la roche n’a pas échangé d’atomes avec son environnement. S’il y a eu un apport ou un retrait d’atomes, cela fausse les résultats. Autrement dit, il doit supposer que la roche ou le minéral a été un système fermé. A priori, on peut considérer que c’est le cas. Les minéraux sont des solides dans lesquels les atomes sont prisonniers. Deux phénomènes sont capables d’en changer la composition : le métamorphisme et la métasomatose. Le premier est la transformation de la roche sous haute température ou pression. Le second résulte de la circulation de fluides qui apportent ou retirent des éléments, grâce aux fissures ou aux pores. Fort heureusement, les géologues peuvent voir si de tels événement se sont produits. Cela requiert une analyse approfondie de la roche.

Utilisation de cristaux de zircon

Le cas du zircon est le plus facile à traiter. C’est un minéral qui apparaît quand un magma acide ou intermédiaire se solidifie : il comprend plus de 52 % de silice SiO₂. Les granites proviennent de magmas acides, avec plus de 65 % de silice. Les zircons n’y sont pas les minéraux principaux, mais ils sont présents, et bien qu’ils soient microscopiques, on arrive à les analyser. Ce minéral est du silicate de zirconium ZrSiO₄, mais quand il cristallise, d’autres éléments (des impuretés) sont incorporés en petites quantités. Des atomes d’uranium se substituent souvent aux atomes de zirconium, or c’est un élément radioactif qui se transforme, par une suite de réactions nucléaires, en plomb. Plus précisément, l’uranium 238 devient du plomb 206 avec une demi-vie de 4,47 milliards d’années et l’uranium 235 devient du plomb 207 avec une demi-vie de 704 millions d’années. En revanche, le zircon n’incorpore pas de plomb. On peut donc être sûr que F(0) = 0. Tous les atomes de plomb présents dans ce minéral proviennent de la désintégration radioactive de l’uranium. Pour compléter le tableau, on peut mentionner la présence de thorium 232, qui se désintègre en plomb 208 avec une demi-vie de 14 milliards d’années.

La photo montre un zircon, dans du granite, observé au microscope polarisant. La roche a été coupée et réduite à une lame très mince, de 30 µm (micromètre) d’épaisseur. La lumière traverse un polariseur, puis la lame, puis un deuxième polariseur. Si l’échantillon de roche était absent, la lumière serait totalement absorbée par les polariseurs, et tout serait donc noir. Les cristaux font tourner la direction de polarisation de la lumière. Le zircon apparaît avec des teintes vives qui lui sont caractéristiques. On voit qu’il est automorphe : il a des faces planes parce qu’il a pu croître librement dans le magma. Les zircons figurent parmi les premiers cristaux à se former. Ils sont souvent inclus dans de la biotite (mica noir), qui est l’un des principaux constituants des granites. Au fil du temps, ils s’entourent de halos noirs, dus à la destruction du réseau cristallin de la biotite par la radioactivité. Sur la photo, ce halo n’est pas encore présent. De plus, une zonation est visible : on a l’impression de voir plusieurs cristaux emboîtés. Les faces planes et la zonation sont caractéristiques des cristaux jeunes, qui n’ont pas été transformés.

Les zircons sont quasiment inaltérables. Ils peuvent résister à des épisodes de métamorphisme mais perdent leur zonation et acquièrent une forme arrondie. Si la roche dans laquelle ils sont nés est détruite par l’érosion, ils subsistent et se retrouvent dans d’autres roches.

Les spectromètres de masse permettent de déterminer la composition des zircons, malgré leur taille microscopique. On mesure les rapports entre les quantités de plomb et d’uranium. Par précaution, on prend les deux rapports ²⁰⁶Pb/²³⁸U et ²⁰⁷Pb/²³⁵U, qui correspondent au rapport F(t)/P(t) de la formule. Si les deux rapports donnent les mêmes âges, tout va bien. On dit qu’ils sont concordants. Sinon, c’est que le zircon n’a pas toujours été un système fermé, mais on peut quand même déterminer l’âge de l’échantillon de roche d’où il a été extrait.

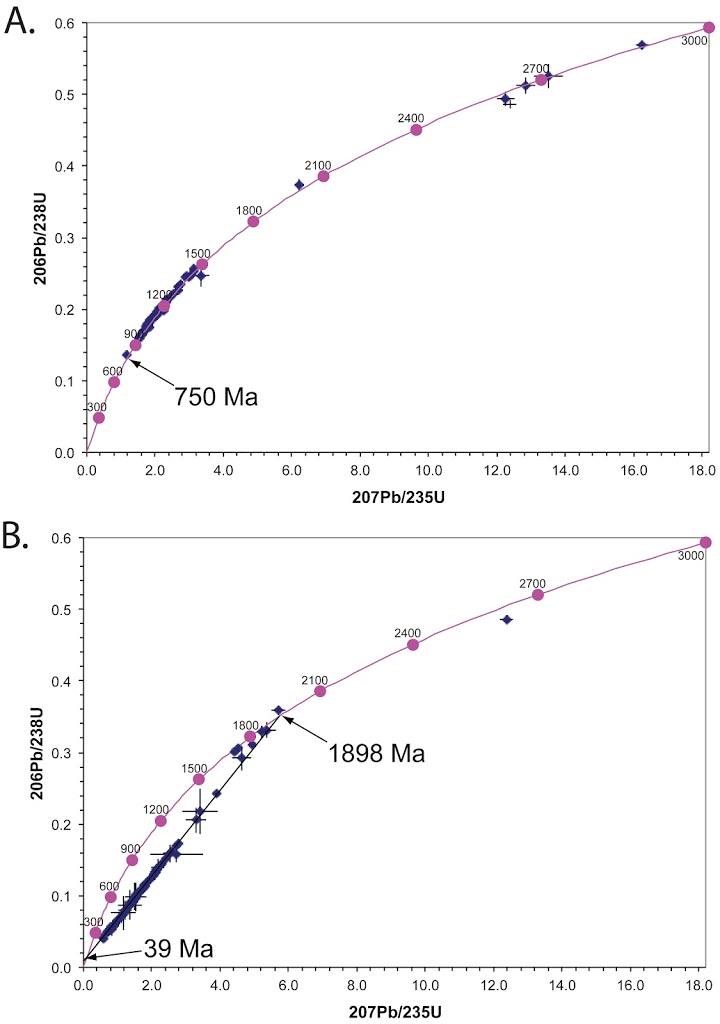
On trace une courbe théorique, toujours basée sur cette formule, dans un diagramme où les rapports ²⁰⁷Pb/²³⁵U et ²⁰⁶Pb/²³⁸U sont en abscisse et en ordonnée. On obtient une courbe qui est paramétrée par le temps, appelée « concordia ». Au temps 0, il n’y a pas de plomb et les deux rapports sont nuls. Ils augmentent ensuite de la manière qui est indiquée. À 3 milliards d’années, le rapport ²⁰⁷Pb/²³⁵U est de 18 et le rapport ²⁰⁶Pb/²³⁸U est de 0,6. On prend ensuite un cristal de zircon et on le place sur le diagramme grâce à ses deux rapports. Si les âges sont concordants, le point obtenu tombe sur la courbe concordia.

Sur le premier diagramme, figure une collection de zircons de la formation Big Cottonwood dans l’Utah. Elle comporte des quartzites surmontées d’ardoises. Ce sont des sédiments métamorphisés. Les zircons tombent tous sur la courbe concordia, mais leurs âges s’échelonnent entre 750 millions d’années et 2,9 milliards d’années. Cela signifie qu’ils proviennent tous de roches qui ont été détruites, certaines très anciennes. Ils se sont retrouvés dans des sables quartzeux et ce dépôt s’est achevé il y a 750 millions d’années. C’est un âge précambrien.

Sur le deuxième diagramme, figure une collection de zircons de l’Himalaya indien. Ils ont été prélevés dans des granites métamorphisés de la formation Munsiari. Cette fois, leurs âges ne sont pas concordants. Ils sont alignés sur une droite appelée « discordia ». L’explication est qu’ils ont perdu du plomb. Il y a eu deux épisodes de métamorphisme, le dernier dû à la surrection de l’Himalaya. Il est normal que les zircons perdent du plomb dès que l’occasion s’en présente, puisque ce métal est malvenu dans leur réseau cristallin. Or quand du plomb est expulsé, les deux rapports ²⁰⁶Pb/²³⁸U et ²⁰⁵Pb/²³⁵ baissent. On peut pourtant lire l’âge de l’échantillon de roche : c’est l’intersection supérieure de la courbe concordia et de la droite discordia. Cet âge est de 1,898 milliard d’années.

Méthode de l’isochrone.

Que faire si la roche ne contient pas de zircon, comme c’est le cas du basalte, dont le taux de silice est inférieur à 52 % ? On utilise une autre méthode, comme celle du couple rubidium/strontium. Le rubidium est un métal alcalin, de même que le sodium et le potassium. Il possède deux isotopes naturels, ⁸⁵Rb et ⁸⁷Rb. Le second se désintègre par radioactivité bêta en strontium 87 avec une demi-vie de 48,81 milliards d’années. Le problème est toujours de déterminer l’âge de la roche, à partir du moment où elle s’est formée par solidification d’un magma. Cette fois, on ne connaît pas la quantité d’éléments fils F(0) = ⁸⁷Sr(0) qui a été incorporée dans la roche, mais on considère un isotope stable, ⁸⁶Sr, et l’on sait qu’au temps 0, quand le magma s’est solidifié, le rapport ⁸⁷Sr/⁸⁶Sr était le même dans tous les minéraux constituant la roche. Cette subtilité est importante. Des minéraux différents, en cours de cristallisation, n’incorporent pas forcément les mêmes teneurs de strontium (qui se comporte comme le calcium), mais le rapport entre les isotopes de cet élément est le même partout. On dit qu’il n’y a pas de fractionnement isotopique. Cela se vérifie en laboratoire.

De plus, on admet que la quantité d’isotope stable ⁸⁶Sr n’a varié nulle part dans la roche au cours du temps : ⁸⁶Sr(t) = ⁸⁶Sr(0). On peut donc diviser l’équation

F(t) = F(0) + P(t) [exp (λt) ‒ 1]

par la quantité de ⁸⁶Sr :

(⁸⁷Sr/⁸⁶Sr)(t) = (⁸⁷Sr/⁸⁶Sr)(0) + (⁸⁷Rb/⁸⁶Sr)(t) [exp (λt) ‒ 1].

Le nombre Y₀ = (⁸⁷Sr/⁸⁶Sr)(0) est inconnu mais on n’a pas besoin de le déterminer. Il faut juste savoir que c’est une constante, grâce à l’absence de fractionnement isotopique. En revanche, les rapports Y = (⁸⁷Sr/⁸⁶Sr)(t) et X = (⁸Rb/⁸⁶Sr)(t) varient selon les minéraux analysés. Cette équation est donc celle d’une droite dont la pente est [exp (λt) ‒ 1] :

Y = [exp (λt) ‒ 1] X + Y₀.

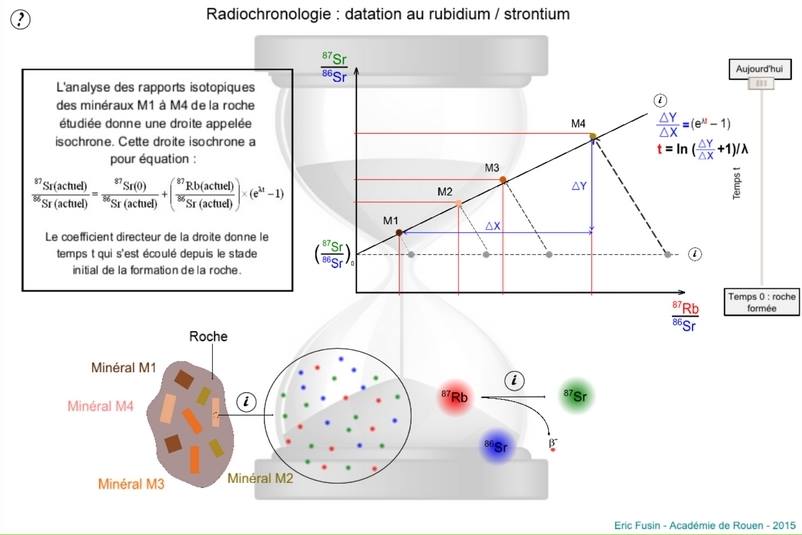
On l’appelle la droite isochrone. Pour tracer une droite, il faut en connaître deux points. Les rapports Y et X doivent donc être mesurés dans deux minéraux différents. Afin d’obtenir un bon résultat, on effectue un plus grand nombre de mesures. La pente de la droite étant connue, on calcule l’âge t de la roche.

Cette illustration illustre la démarche :