L’effet de serre a été pressenti en 1824 par le mathématicien français Joseph Fourier (1768-1830), dans sa tentative d’expliquer le bilan énergétique de la Terre. Il a écrit que la lumière du Soleil atteint facilement la surface de la Terre mais que les infrarouges (la chaleur obscure, comme on disait à l’époque) qu’elle émet vers l’espace franchissent plus difficilement l’atmosphère. On sait depuis quelques années qu’en 1857, l’Américaine Eunice Newton Foote (1819-1888) a démontré le rôle du dioxyde de carbone. Elle a observé que des cylindres de verre remplis de CO2 s’échauffaient plus à la lumière du Soleil que des cylindres n’en contenant pas. Le rôle du CO2 dans ce qui n’était pas encore appelé l’effet de serre était mis en évidence. Ses expériences ont été éclipsées par celles de l’Irlandais John Tyndall (1820-1893). En 1861, il a démontré le rôle de la vapeur d’eau en plus du CO2.
Le réchauffement climatique étant l’un des grands problèmes auxquels l’humanité est confrontée, il est indispensable que ce phénomène physique soit correctement compris. J’ai déjà parlé de l’effet de serre radiatif dans cet article, de manière très détaillée, quoique sans formule mathématique, ainsi que dans l’article consacré à l’empreinte de l’activité humaine sur la troposphère et la stratosphère. Mon objectif était d’expliquer la conséquence d’une augmentation de la teneur en CO2 atmosphérique. Le but du présent article est de présenter l’effet de serre d’une manière plus basique (du moins, au début). Il est aussi de lutter contre la désinformation, la science du climat étant confrontée à un puissant mouvement de déni alimenté par des intérêts financiers et politiques. Certains de ces « climatosceptiques », qu’il serait préférable d’appeler climato-dénialistes, vont jusqu’à nier l’existence même de l’effet de serre.

Parmi eux figure l’ingénieur et entrepreneur retraité Jacques-Marie Moranne, secondé par le polytechnicien Camille Veyres. En 2019, ils ont mis en ligne un ouvrage intitulé La physique du climat, qui est truffé d’erreurs. Certaines sont faciles à corriger, mais parfois, c’est plus difficile. On peut comprendre que ces ingénieurs, dont la formation en physique est basique, n’aient pas compris certaines subtilités. Il faudra donc les expliquer ici.
On lira avec profit l’article de Jean-Louis Dufresne et Jacques Treinet, l’effet de serre est plus subtil qu’on ne le croit, qui, eux, connaissent vraiment ce sujet.
Rayonnement absorbé et émis par la Terre
La surface de la Terre est chauffée par le rayonnement solaire, comprenant essentiellement des ultraviolets, de la lumière et des infrarouges. Les sources internes de chaleur, dont le volcanisme, sont parfaitement négligeables. Tous les rayonnements électromagnétiques contiennent de l’énergie, d’autant plus que leurs longueurs d’onde sont courtes, et les corps qui les absorbent sont chauffés : l’agitation des atomes ou des molécules qui les composent augmente. Autrement dit, l’énergie de ces rayonnements est transformée en énergie cinétique. Il n’y a jamais de création ni de perte d’énergie.
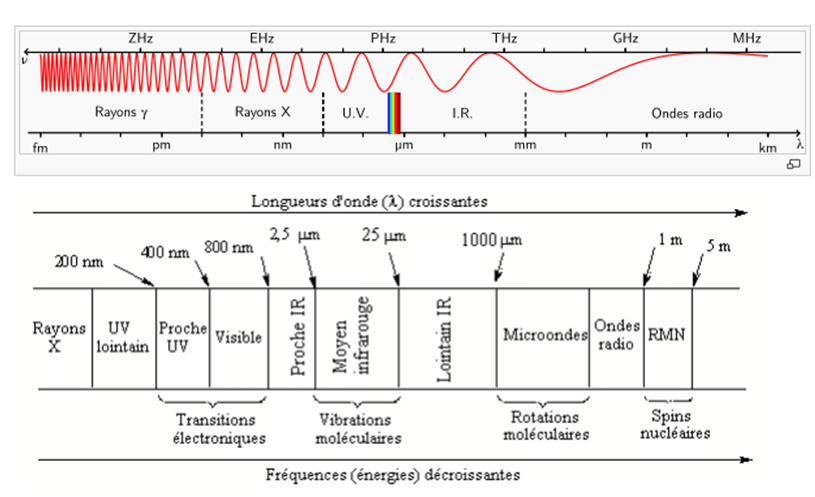
Comme la Terre est chauffée, elle renvoie cette énergie dans l’espace sous forme d’infrarouges thermiques. Tous les corps chauffés en émettent. S’ils émettent plus de rayonnements qu’ils n’en reçoivent, ils se refroidissent. Dans le cas contraire, ils se réchauffent. Un corps est en équilibre thermique s’il émet autant d’énergie qu’il en reçoit. Dans ce cas, sa température est constante.
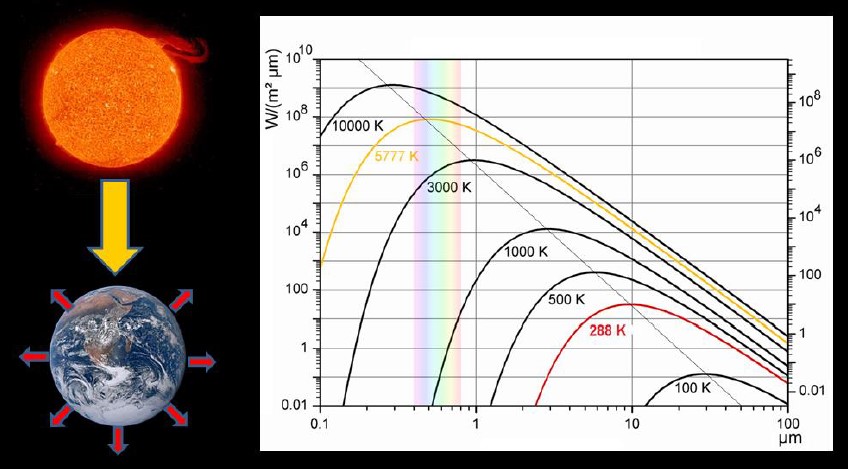
La Terre reçoit 1 361 W/m² (watts par mètre carré) de rayonnement solaire. Plus exactement, un disque de rayon R, où R est le rayon de la Terre, perpendiculaire aux rayons du Soleil, reçoit une puissance de 1 361 watts sur chaque mètre carré. La surface de ce disque vaut πR². Mais cette énergie est répartie sur toute la surface de la Terre, qui vaut 4πR². Il faut donc diviser 1 361 par 4 pour obtenir le flux solaire incident que la surface de la Terre reçoit. On trouve 340 W/m² avec un arrondi à l’unité. Bien sûr, il s’agit d’un flux moyen, une moitié de la Terre n’étant pas éclairée du tout. Notre planète en réfléchit 100 W/m², si bien que seuls 240 W/m² sont absorbés et permettent son chauffage. Sur la Terre, contrairement à la lumière, les infrarouges ne sont jamais réfléchis. Ils sont absorbés la surface des océans, qu’ils contribuent à chauffer.
Le flux rayonné par un corps chauffé à une température T est donné par une loi établie expérimentalement par Joseph Stefan en 1879 et expliquée par Ludwig Boltzmann en 1884. Elle dit que la puissance totale par unité de surface dans le demi-espace libre (radiance R ou émittance énergétique ou exitance énergétique) rayonnée vaut eσT4 watts par mètre carré, où e est l’émissivité de ce corps, σ est la constante de Stefan-Boltzmann, égale à
5,67 × 10–8 W/(m²·K4)
et T est exprimée en kelvins (à partir du zéro absolu, en retranchant 273,15 aux degrés Celsius). L’émissivité est un nombre toujours compris entre 0 et 1. Si elle est égale à 1, le corps est un émetteur parfait. L’émissivité de la Terre est proche de 1.

Températures d’équilibre de la Terre et de la Lune
La Terre est en équilibre thermique si elle émet 240 W/m² d’infrarouges thermiques dans l’espace. Elle envoie alors autant d’énergie dans l’espace qu’elle en reçoit du Soleil. Pour calculer sa température d’équilibre, dite température effective et notée Te, on écrit donc que σ Te4 = 240 K et on trouve que Te est égale à 255 K , ou encore – 18 °C. Une émissivité inférieure à 1 donne une température supérieure. Pour e = 0,9, on a T= – 11°C.
Évidemment, pour que ce résultat ait un sens, il faut supposer que la surface de la Terre est isotherme, c’est-à-dire partout à la même température. Ce n’est exactement le cas, mais comme la Terre tourne rapidement sur elle-même et possède une grande inertie thermique, surtout grâce aux océans, il n’y a en moyenne que 10 °C de différence entre le jour et la nuit. Il faut se rappeler que l’on devrait utiliser les degrés Kelvin, parce qu’ils partent du zéro absolu. On peut considérer que la température de surface des océans varie entre 0 °C et 30 °C, donc entre 273 K et 303 K, en négligeant les décimales. Cela fait une variation de 10 %.
Puisque la Terre possède une atmosphère, sa température de surface n’est pas égale à – 18 °C. L’effet de serre radiatif en est responsable, mais avant d’en parler, il convient de remarquer la présence à côté de la Terre d’un astre éclairé comme lui et qui n’a pas d’atmosphère : la Lune. Si l’on calcule sa température de surface moyenne, trouve-t-on – 18 °C ? Non, d’abord parce que l’albédo a de la Lune n’est pas égal à 0,29, mais à 0,11. Elle absorbe plus de rayonnement solaire que la Terre et devrait être en moyenne plus chaude. Pour calculer sa température effective Te, il faut écrire que σ Te4 est égal à (1 – a) × 340, ce qui donne Te = 270 K, soit – 3 °C.
Ensuite, l’hypothèse de l’isothermie n’est plus possible. À la surface de la Lune, il y a d’énormes variations de température en fonction de la latitude et de l’heure. Rien n’empêche de calculer sa température moyenne globale, mais on trouve un résultat très bas : – 72 °C (201 K). Cette estimation a été présentée par Gerhard Kramm, Nicole Mölders et Ralph Dlugi dans un article publié en 2022.
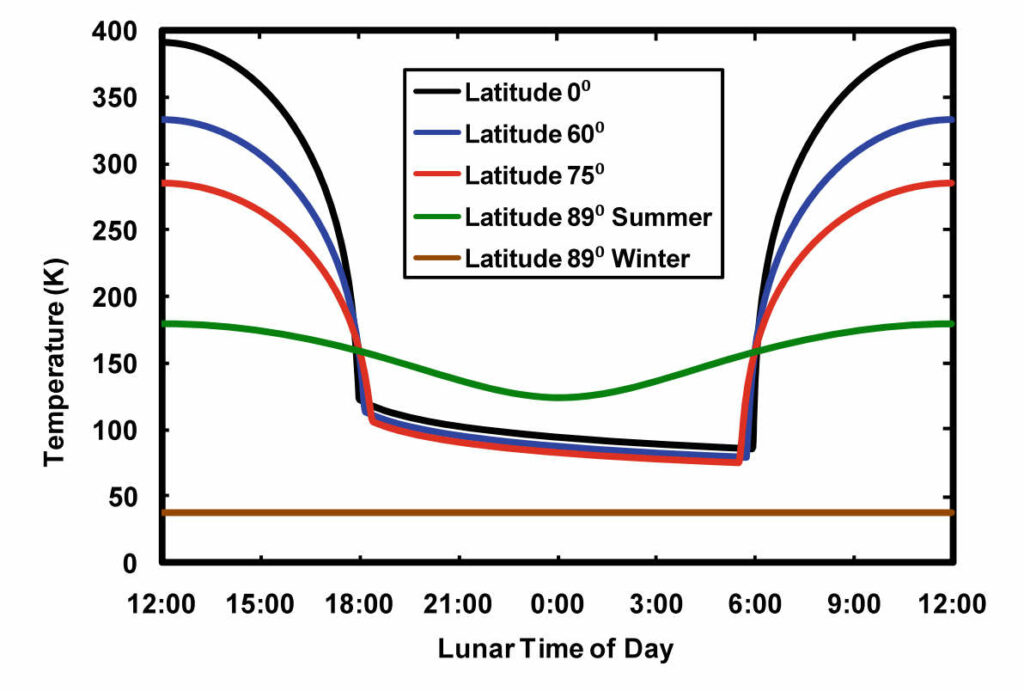
Elle utilise les mesures effectuées par un radiomètre infrarouge appelé DLRE (Diviner Lunar Radiometer Experiment) embarqué à bord de la sonde Lunar Reconnaissance Orbiter, lancée le 18 juin 2009 . En avril 2015, on disposait de 250 milliards de mesures calibrées. On pourra consulter les résultats dans cet article de J.-P. Williams, D.A. Paige et deux autres scientifiques, publié en 2017.
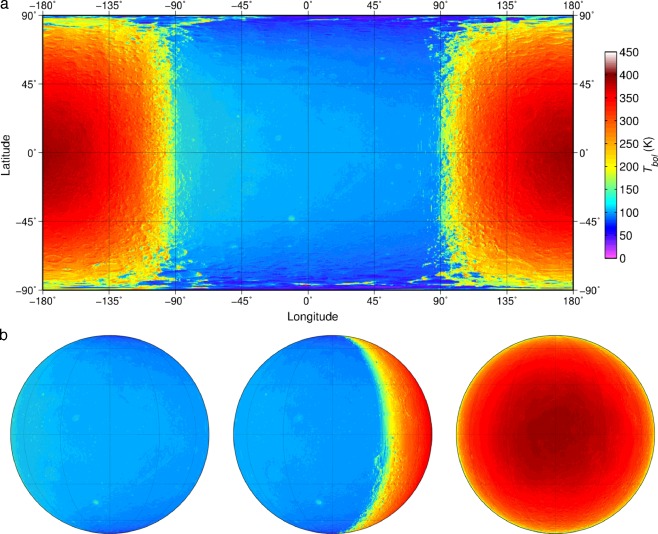
Les températures ainsi mesurées sont des températures bolométriques, qui sont un peu différentes des températures réelles. Ce que Kramm et al. ont calculé est donc leur moyenne <Tbol>. Mais ce n’est que la moyenne arithmétique d’un ensemble de nombres. On pourrait dire qu’elle n’a pas de signification physique. Comme on parle des échanges de rayonnements entre la surface et l’espace, il est plus pertinent de prendre la moyenne des flux émis par la surface. Cela revient à calculer la moyenne desT4, or on obtient un résultat toujours inférieur quand on calcule la moyenne des T et qu’on l’élève ensuite à la puissance 4. La température effective Te,M que Kramm et al. ont calculé pour la Lune vaut – 2 °C (271 K) :
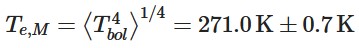
La température moyenne globale <Tbol> lui est inférieure de 70 K. On retrouve presque la valeur de 270 K donnée ci-dessus après un calcul beaucoup plus court.
En 2013, un scientifique de la NASA, Robert M. Haberle, a proposé de modifier la définition utilisée jusque-là de l’effet de serre, en disant qu’il fallait prendre la température effective de surface Tes au lieu de la température moyenne globale annuelle pour évaluer l’effet de serre sur un astre doté d’une atmosphère, la seconde étant toujours inférieure à la première. Son article était consacré à Mars, qui est peu éclairée parce que plus éloignée du Soleil que la Terre, possède une atmosphère très tenue et a d’importantes différences de températures de surface. Pour un ciel dégagé, l’effet de serre Tse – Te calculé est de 5,13 K, alors qu’avec l’ancienne définition, il est de – 8,82 K.
On peut s’étonner que la communauté scientifique ait attendu 2013 pour donner la bonne définition d’un phénomène connu depuis si longtemps. Quant aux climato-dénialistes qui nient l’existence de l’effet de serre, ils insistent sur le fait que seule la température moyenne globale compte. Ils s’efforcent de fournir pour la Terre des estimations inférieures à 255 K (– 18 °C) : 144 K pour Gerlich et Tscheuschner, entre 195 et 200 K pour Nikolov et Zeller, entre 159 et 237 K pour Moranne. Ainsi, une Terre sans atmosphère serait très froide et l’atmosphère n’arriverait pas à la chauffer jusqu’à 288 K (15 °C) grâce à l’effet de serre. Kramm et al. sont peu susceptibles de vouloir en exagérer l’importance, car ils ont défendu Gerlich et Tscheuschner et les ont cités, en corrigeant cependant quelques erreurs flagrantes.
L’effet de serre
La surface de la Terre émet un flux d’infrarouges thermiques dont la moyenne vaut 398 W/m². Il correspond à une température effective de surface Tse de 16°C (289 K). Une partie de ce flux est retenu par l’atmosphère, si bien que seuls 240 W/m² arrivent à s’échapper dans l’espace. Ce flux correspond à la température effective Te de – 18 °C (255 K). La différence Tse – Te = 34 °C traduit l’action des nuages et des gaz à effet de serre (GES) présents dans l’atmosphère terrestre, essentiellement de la vapeur d’eau, du CO2 et de l’ozone O3. Le méthane CH4, un autre GES, ne doit sa présence qu’à l’activité humaine. Il s’agit d’un phénomène naturel que l’humanité ne fait qu’amplifier, sans lequel la Terre serait gelée.
On peut aussi définir l’effet de serre comme la différence entre le flux émis par la surface et le flux sortant de l’atmosphère : 398 – 240 = 158 W/m². C’est le flux retenu par l’atmosphère.
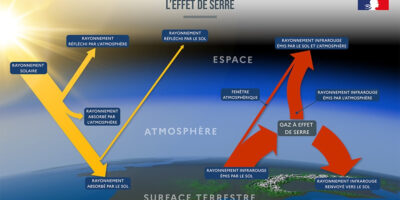
Le principe de l’effet de serre est simple : les infrarouges thermiques émis par le sol sont partiellement absorbés par les gaz à effet de serre et les nuages, puis ils sont réémis à la fois vers le sol (on parle de rétro-rayonnement) et vers l’espace. Cela provoque une hausse de la température d’équilibre à la surface de la Terre.
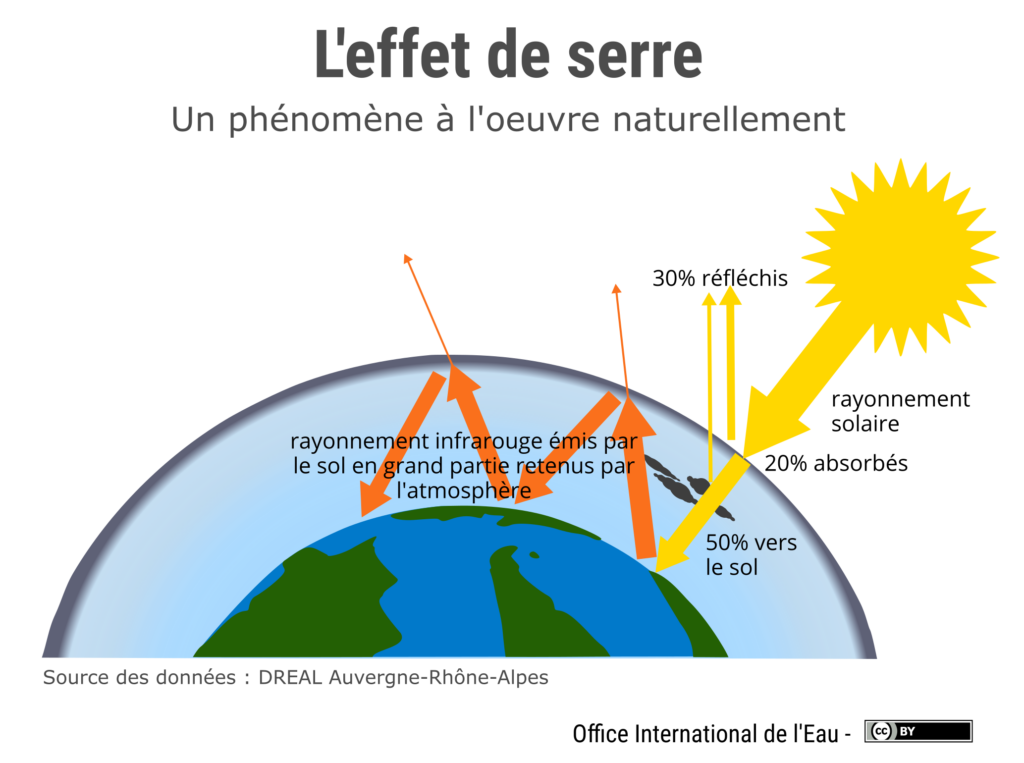
J.-M. Moranne et d’autres climato-dénialistes nient l’existence de ce rétro-rayonnement alors qu’il peut être mesuré grâce à un détecteur infrarouge (un pyrgéomètre, par exemple) et analysé grâce à la spectroscopie infrarouge.
En première approximation, les nuages et les gaz à effet de serre peuvent être assimilés à une vitre qui retient les infrarouges émis par le sol. Entre la vitre et le sol, il y a donc une accumulation de chaleur. Ceux qui disent que cette approximation est fausse parce que la Terre n’est pas recouverte d’une vitre ne comprennent pas ce qu’est la physique. On présente toujours des modèles simplifiés des systèmes que l’on étudie, qui permettent de faire quelques calculs simples. Ainsi, l’atome d’hydrogène est d’abord assimilé à un électron tournant autour d’un proton, alors que, selon la mécanique quantique, il n’y a pas d’électron mais un « nuage de probabilités ».
On suppose que la vitre reçoit 340 W/m² de rayonnement solaire. Elle réfléchit 100 W/m² et laisse passer 240 W/m². Le rayonnement transmis est absorbé par le sol, qu’il chauffe. Celui-ci émet 240 W/m² d’infrarouges thermiques, dont les longueurs d’ondes sont plus grandes que celles du rayonnement solaire. Ils arrivent sur la vitre et sont absorbés par elle. Elle émet à son tour des infrarouges thermiques, mais la moitié vers le haut et la moitié vers le bas, soit deux fois 240/2 W/m². Par conséquent, 120 W/m² s’échappent dans l’espace. Le reste retourne vers le sol et accroît sa température, si bien qu’il émet 120 W/m² de plus. Ces infrarouges sont interceptés par la vitre, qui en réémet une moitié (240/4 W/m²) et en laisse échapper 60 W/m² dans l’espace. Et ainsi de suite.
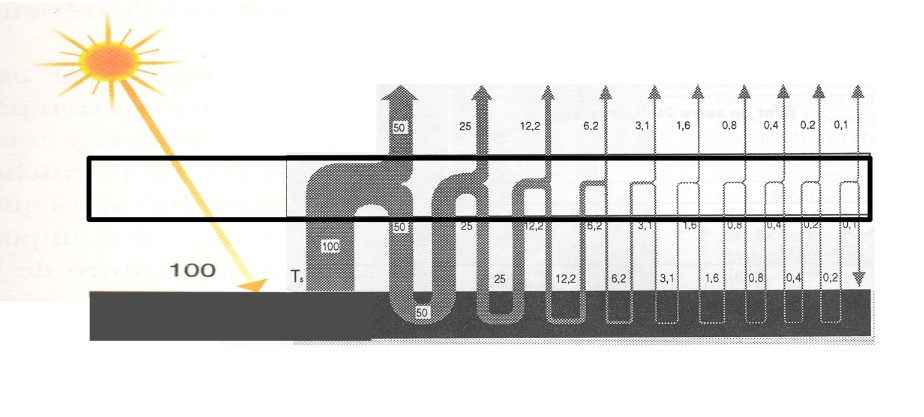
Le sol reçoit par conséquent 240 + 240/2 + 240/4 + … W/m². On reconnaît une série géométrique de raison 1/2 . La somme infinie 1+ 1/2 + /1/4 + 1/8 + … vaut 2, si bien que ce sont 480 W/m² (240 × 2) qui sont absorbés par le sol. Quant à la vitre, elle émet dans l’espace 120 + 120/2 + 120 /4 + … W/m², ce qui fait 240 W/m². Il en résulte que le système renvoie dans l’espace autant d’énergie qu’elle en reçoit, mais que la température d’équilibre du sol est plus élevée que sans la vitre. Elle est multipliée (en degrés kelvin !) par la racine quatrième de 2, soit 1,19. La température d’équilibre de la Terre est alors de 303 K au lieu de 255 K, soit 30 °C au lieu de – 18 °C. C’est trop chaud mais on sait que ce modèle est approximatif.
En fin de compte, la Terre reçoit 340 W/m² de rayonnements à ondes courtes (ultraviolets, lumière et infrarouges proches). Elle en réfléchit 100 W/m². La vitre, symbolisant les nuages et les gaz à effet de serre, émet 240 W/m² d’infrarouges vers l’espace. Elle renvoie également 240 W/m² d’infrarouges vers le sol, qui correspondent au rétro-rayonnement, si bien que le sol en absorbe au total 480 W/m². Il est autant chauffé par la vitre que par le Soleil. Comme il est en équilibre thermique, il doit émettre 480 W/m², dont seule une moitié s’échappe dans l’espace.
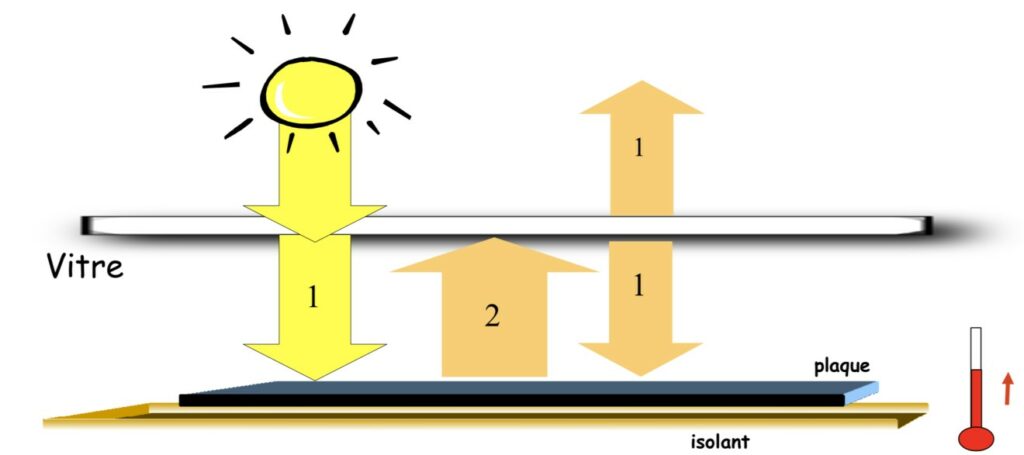
Dans ce système, alors que le sol est à 30 °C, la vitre est à – 18 °C. Cela se déduit du fait qu’elle rayonne 240 W/m² d’infrarouges. On pourrait penser que la vitre chauffe un corps plus chaud qu’elle (le sol), ce qui paraîtrait choquant. D’après le deuxième principe de la thermodynamique, dans un système isolé, la chaleur va toujours du corps le plus chaud vers le corps le plus froid. Mais c’est oublier qu’une moitié de la chaleur reçue par le sol provient directement du Soleil. On a supposé que son rayonnement n’est pas absorbé par la vitre. Il ne peut donc pas la chauffer. En réalité, le sol chauffe la vitre, grâce aux infrarouges qu’il émet et qui sont absorbés par elle, mais cela n’exclut pas du tout l’existence du rétro-rayonnement de la vitre vers le sol, preuve de l’existence de l’effet de serre.
Nuages et gaz à effet de serre
Les nuages sont constitués de gouttelettes d’eau ou de cristaux de glace. Ils peuvent être refroidissant, car ils réfléchissent le rayonnement solaire, et réchauffant, parce qu’il exerce un effet de serre. Les cirrus, nuages de haute altitude, absorbent peu de rayonnement solaire mais absorbent une large part des infrarouges thermiques émis par la surface de la Terre. Ils se comportent donc presque comme la vitre du paragraphe précédent. Un cirrus de 100 mètres d’épaisseur (très fin) ne réfléchit qu’environ 9 % de la lumière solaire mais empêche presque 50 % des infrarouges thermiques de s’échapper dans l’espace. Il n’est alors pas difficile de comprendre que ces nuages ont un pouvoir réchauffant. Sous les cirrus, la température est en moyenne élevée de 10 °C, or ils couvrent un peu plus de 30 % de la surface de la Terre, jusqu’à 70 % sous les tropiques pendant la nuit. Ce sont pourtant des nuages froids, puisque leur altitude va de 7 000 m aux latitudes moyennes à 13 500 m sous les tropiques. Ils sont constitués de cristaux de glace dont la température est habituellement inférieure à – 20 °C. Au-dessus de – 68 °C, la plupart des cirrus ont une humidité relative de près de 100 % (air saturé en vapeur d’eau).

Les GES fonctionnent de la même manière que les cirrus, sauf qu’ils sont présents jusqu’au niveau de la mer (sauf l’ozone stratosphérique) et qu’ils n’absorbent pas les infrarouges dans toutes les longueurs d’onde. Ils ont des bandes d’absorption. Ainsi, le CO2 est particulièrement actif autour de 15 µm (micromètres), mais cela lui donne un rôle important, car c’est là que se situe le pic d’émission des infrarouges thermiques de la surface de la Terre. Ceux-ci ont des longueurs d’onde comprises entre 5 et 100 µm. Une autre bande d’absorption du CO2, autour de 4,25 µm, n’arrête donc presque pas ces infrarouges.
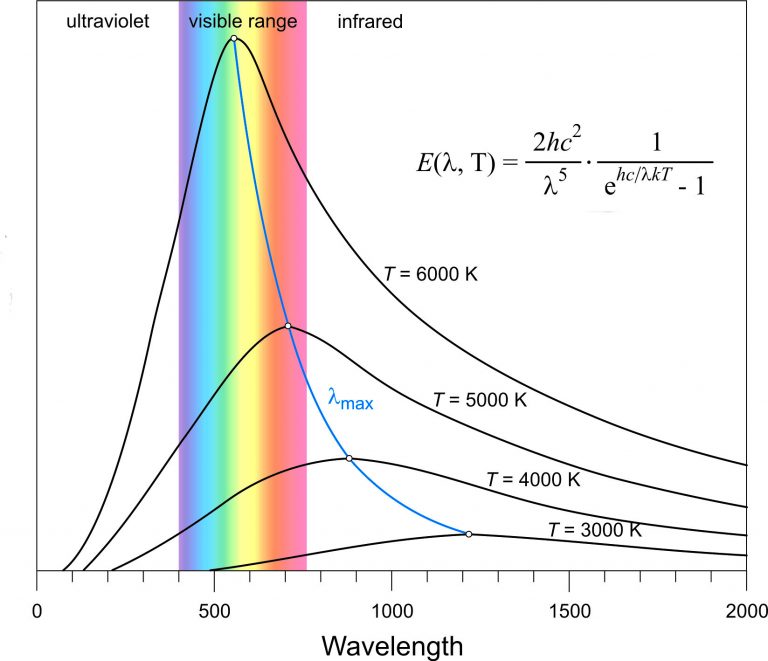
La loi de Stefan-Boltzmann se déduit de la loi de Planck, présentée dans la figure ci-dessus. Elle a valu au physicien Max Planck le prix Nobel de physique, en 1918, et a jeté les bases de la physique quantique. Elle donne le flux énergétique émis par la surface d’un corps pour une longueur d’onde particulière (et par unité de surface, d’angle solide et de longueur d’onde). On parlera ici de luminance spectrale. Pour une température donnée, en mettant la longueur d’onde en abscisse, on obtient une courbe. L’aire de cette courbe (son intégrale, en langage mathématique) multipliée par le nombre π est sa radiance.
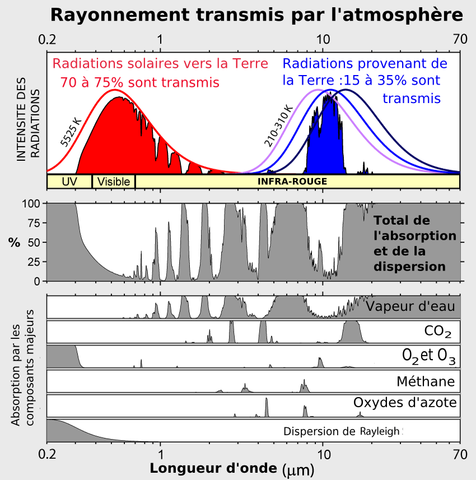
La figure ci-dessus donne la luminance spectrale d’un corps noir à 5 525 K (courbe rouge), ainsi qu’entre 210 et 310 K (courbes bleues). Attention aux échelles ! Les courbes bleues sont très étalées le long de l’axe des abscisses. Alors que les infrarouges sont compris entre 5 et 100 µm, la lumière (visible) est seulement comprise entre 0,38 et 0,78 µm. Il n’empêche que les courbes bleues sont toutes comprises dans la courbe rouge. Dans cette figure, elles sont très étirées en hauteur pour qu’on puisse les voir. Autrement dit, la radiance d’un corps noir à 210-310 K est très inférieure à la radiance d’un corps noir à 5 525 K. Vu la différence de température, c’est assez évident !
On considère que la température effective du Soleil est de 5 772 K (soit environ 5 498 °C). C’est la température d’un corps noir qui aurait sa radiance. Sa puissance totale est de 3,826 × 1026 W. Sachant qu’il a un rayon moyen de 1 392 684 km, sa radiance vaut plus de 15 millions de watts par mètre carré. Heureusement que 149,6 millions de kilomètres nous séparent du Soleil. La Terre ne reçoit par conséquent que 1 361 W/m² de rayonnement solaire – ce que l’on appelle la constante solaire.
L’atmosphère terrestre laisse passer 70 à 75 % du flux solaire incident selon la figure ci-dessus, parce que le pic du rayonnement se trouve dans le domaine visible et que l’atmosphère est en grande partie transparente à la lumière. Le flux absorbé par la surface de la Terre est représenté par la courbe pleine rouge. D’après le bilan radiatif de la Terre, il est de 160 ± 5 W/m². C’est l’aire de cette courbe. Comme l’atmosphère est plutôt opaque aux infrarouges, elle n’en laisse passer que 15 à 35 % (courbe pleine bleue). Le rayonnement qui s’échappe dans l’espace devrait donc être inférieur au flux solaire incident, mais si c’était vrai, ce déséquilibre entraînerait une élévation de la température de surface de la Terre, jusqu’à ce que l’équilibre soit établi. C’est le principe de l’effet de serre.
L’atmosphère réelle
La modélisation de l’atmosphère par une plaque de verre n’est pas capable d’expliquer correctement ce qui se passe quand on augmente la teneur en gaz à effet de serre dans l’atmosphère. Pour cela, il faut la représenter de manière beaucoup plus réaliste, en tenant compte de son épaisseur et de sa structure. Il y a des transferts d’énergie entre ses différentes couches, qui ne sont pas que radiatifs. La convection intervient dans la troposphère, ainsi que l’évaporation de l’eau et la condensation de la vapeur d’eau, mais c’est le rayonnement infrarouge qui est au premier plan. Compte tenu de ces transferts, on trouve que l’atmosphère est, en moyenne, deux fois plus chauffée par la surface de la Terre que par le rayonnement solaire. On voit ainsi que l’approximation de l’atmosphère par une plaque de verre n’est pas complètement fausse.
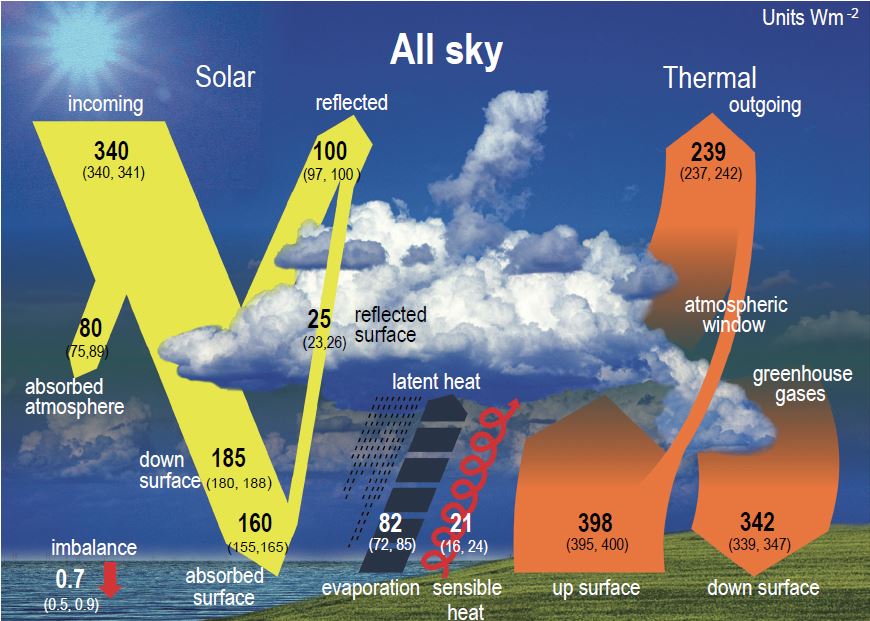
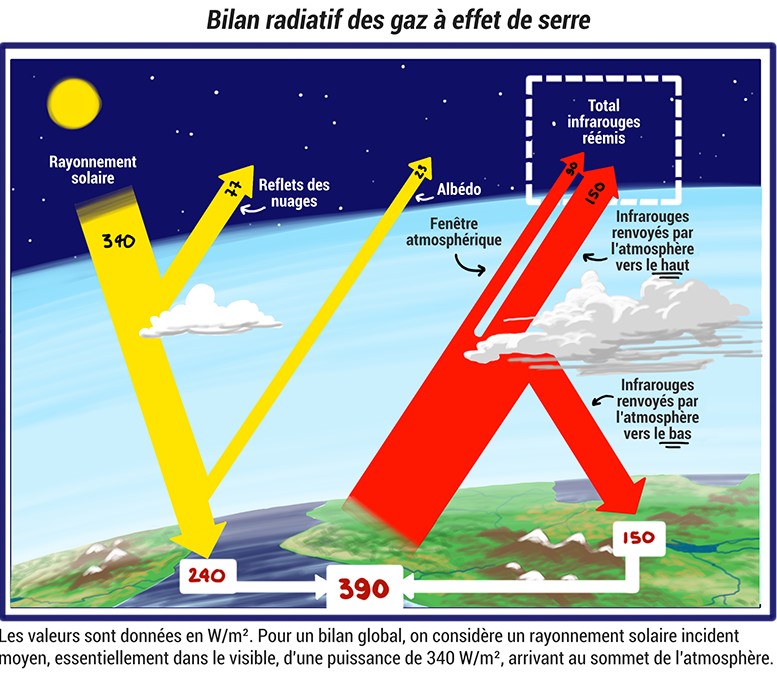
Insister sur le fait que l’atmosphère ne contient « que » 0,042 % en volume de CO2 (en 2024), comme le font les climato-dénialistes, n’a pas de sens, puisque l’azote, l’oxygène et l’argon, constituant 99,96 % de l’atmosphère sèche, ne sont pas des gaz à effet de serre. Le CO2 apporte une contribution d’environ 32 W/m² à l’effet de serre, dont la valeur 158 W/m² a été donnée ci-dessus. Ce n’est pas du tout négligeable.
On va voir que cette « trace » de CO2 rend l’air totalement opaque aux infrarouges à certaines longueurs d’onde.
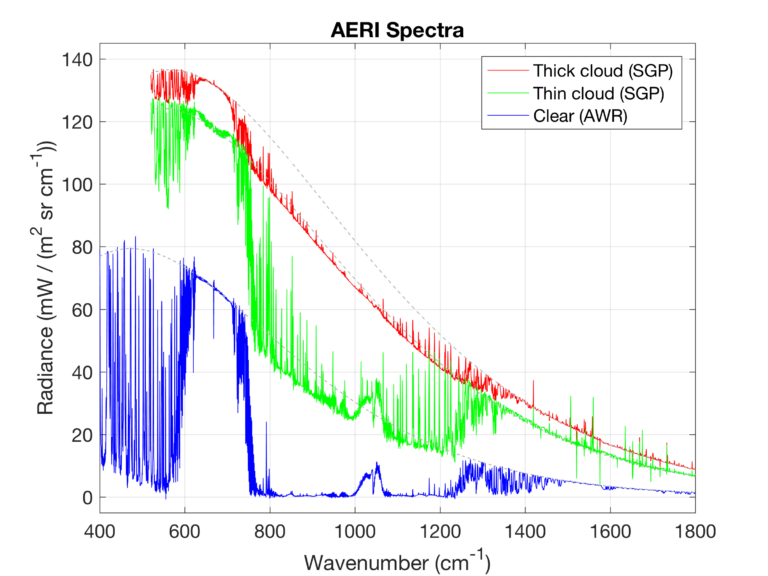
Le graphique ci-dessus montre la luminance spectrale du ciel (en fonction du nombre d’onde) au sud des Grandes Plaines américaines (SGP), en présence de nuages épais (Thick could) et fins (Thin cloud) et dans la base McMurdo en Antarctique (AWR), où le ciel était clair. La bande d’émission autour de 670 cm–1 est celle du CO2 . C’est également une bande d’absorption, puisque les émissions et les absorptions se font aux mêmes nombres d’onde. La droite du graphique est le domaine de la vapeur d’eau. À ces nombres d’onde, les infrarouges sont constamment absorbés et réémis (la réémission est obligatoire, puisque l’air est chauffé ), si bien que ceux qui atteignent le spectromètre ne proviennent que de quelques mètres au-dessus du sol. Ils nous renseignent sur la température juste au-dessus du sol, qui était d’environ – 30 °C à McMurdo. Plus exactement, il s’agit de la température de brillance : celle qu’aurait un corps noir ayant une telle radiance. Cette opacité partielle de la basse atmosphère aux infrarouges la contraint à utiliser la convection comme moyen de transfert d’énergie.
En revanche, l’air est transparent aux infrarouges de nombres d’onde compris entre 800 et 1 200 cm–1 (c’est la fenêtre atmosphérique), sauf dans une bande correspondant à l’ozone, qui est un gaz à effet de serre. Il n’émet ni n’absorbe de rayonnement, si bien qu’en l’absence de nuages, les infrarouges thermiques émis par la surface de la Terre s’échappent dans l’espace et les détecteurs ne captent pas d’infrarouges venus du ciel (à part ceux émis par l’ozone stratosphérique). Quand il y a des nuages, ceux-ci captent les infrarouges qu’ils émettent. Ils peuvent avoir une température de brillance très inférieure à celle de l’air au niveau du sol, comme on le voit avec les nuages fins, puisqu’ils ont des altitudes élevées. Un corps froid peut très bien rayonner vers un corps chaud !
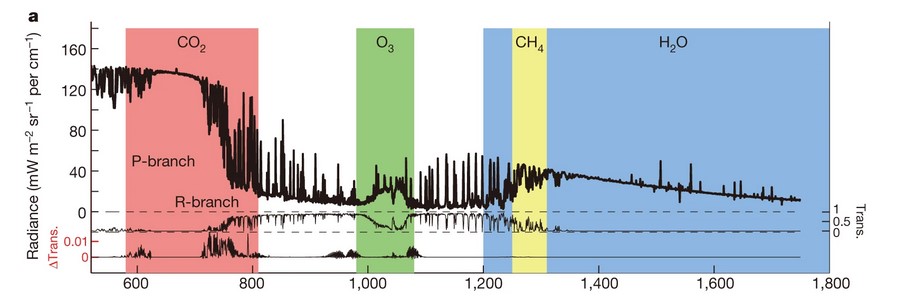
Sur les bords de la bande d’émission (et d’absorption) du CO2, la transmission des infrarouges s’améliore. Cela donne la possibilité d’observer à partir du sol les infrarouges émis par les gaz à effet de serre à des altitudes élevées. La figure ci-dessus donne des observations et des calculs faits par l’équipe de Daniel R. Feldman de l’Université de Californie à Berkeley et présentés dans la revue Nature en 2015. La transmission spectrale (en fonction, ici, du nombre d’onde) est un nombre compris entre 0 et 1. Là où elle vaut 1, les infrarouges ne sont pas absorbés. L’équipe a calculé les variations de la transmission (ΔTrans) causées par l’ajout de CO2 dans l’atmosphère entre 2001 et 2010 : sa concentration est passée de 370 à 392 ppmv (100 ppmv = 0,01 %). Elle a également fait une campagne de mesures avec des AERI, en Alaska et en Oklahoma, qui a mis en évidence une hausse de l’effet de serre dû au CO2 de 0,2 W/m² durant cette décennie. Depuis le début de l’ère industrielle, elle a été de 1,82 W/m².

Une Terre sans gaz à effet de serre non condensables
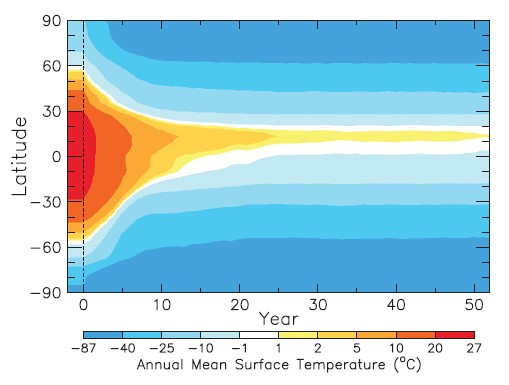
Maintenant que l’on connaît le rôle joué par les gaz à effet de serre, on peut se demander quelle serait la température moyenne globale de la Terre s’ils étaient supprimés. Pour que notre planète reste la Terre, il faut conserver son atmosphère et ses océans, et donc aussi sa cryosphère (ses glaciers) et l’eau de son atmosphère, sous forme solide, liquide et gazeuse. En fait, on supprime seulement les gaz à effet de serre non condensables, dont le CO2. Andrew Lacis, Michael Mann et deux autres chercheurs ont fourni la réponse dans un article publié en 2010. Pour cela, ils ont utilisé un modèle climatique appelé ModelE. Tous ces gaz sont supprimés au temps zéro et l’on regarde comment le système climatique évolue. La figure suivante donne la température moyenne annuelle de surface en fonction du temps, en abscisse, et de la latitude, en ordonnée. L’essentiel du refroidissement se produit durant les 10 premières années. Au bout de 50 ans, la température moyenne globale se stabilise à – 21 °C, après une baisse de 34,8 °C. Les températures moyennes annuelles tombent sous les – 40°C au-delà de 60° de latitude mais elles restent positives à l’équateur, si bien que la Terre n’est pas complètement gelée. La surface occupée par la banquise passe de 4,6 % à 46,7 %, ce qui rend la Terre plus réfléchissante. Son albédo devient 0,42 au lieu de 0,29. Il y a moins de vapeur d’eau dans l’atmosphère mais plus de nuages, qui contribuent à réfléchir le rayonnement solaire. Ils couvrent les trois quarts du globe.
Le cas extrême de Vénus
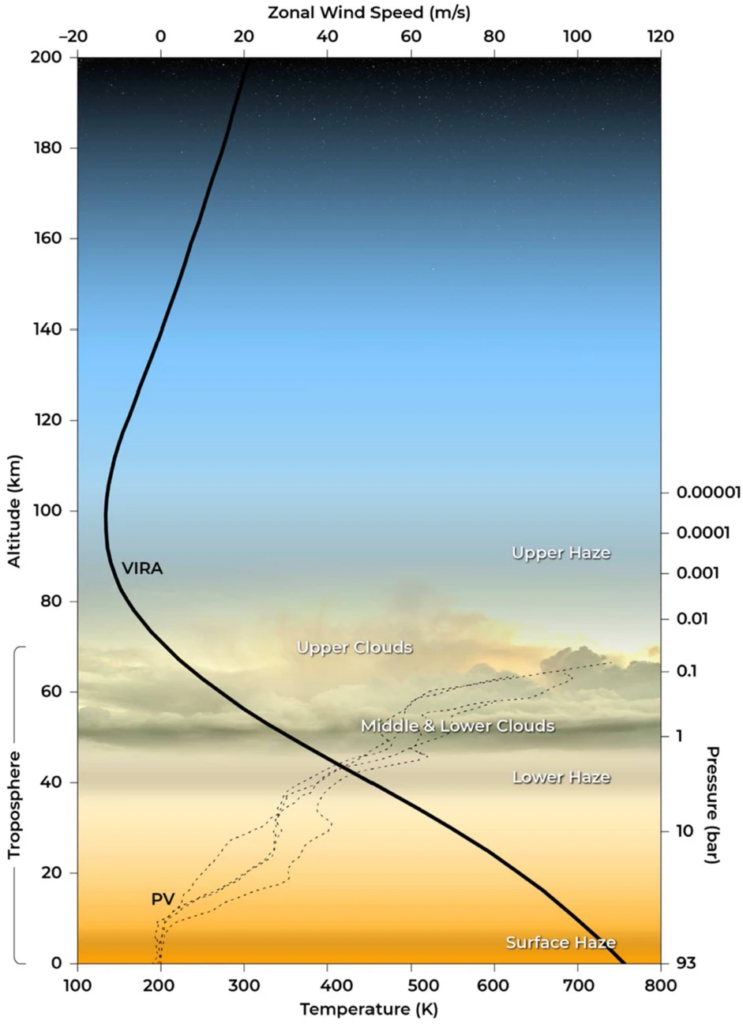
Le CO2 est un constituant naturel des atmosphères planétaires. Sur Terre, il est émis par les volcans, mais il est retiré de l’atmosphère par l’eau et la végétation. D’immenses quantités de carbone sont stockées dans des roches sédimentaires. Sur Vénus, qui est presque dépourvue d’eau, l’atmosphère est composée à 96,5 % de CO2. Elle est 93 fois plus massive que l’atmosphère terrestre et la température au sol varie autour de 462 °C. Elle est homogénéisée par des vents très forts. La constante solaire est de 2 601 W/m² mais l’albédo est de 0,77 à cause de nuages recouvrant toute la planète, si bien que la température de surface (avec une émissivité de 1) devrait être de – 46 °C.
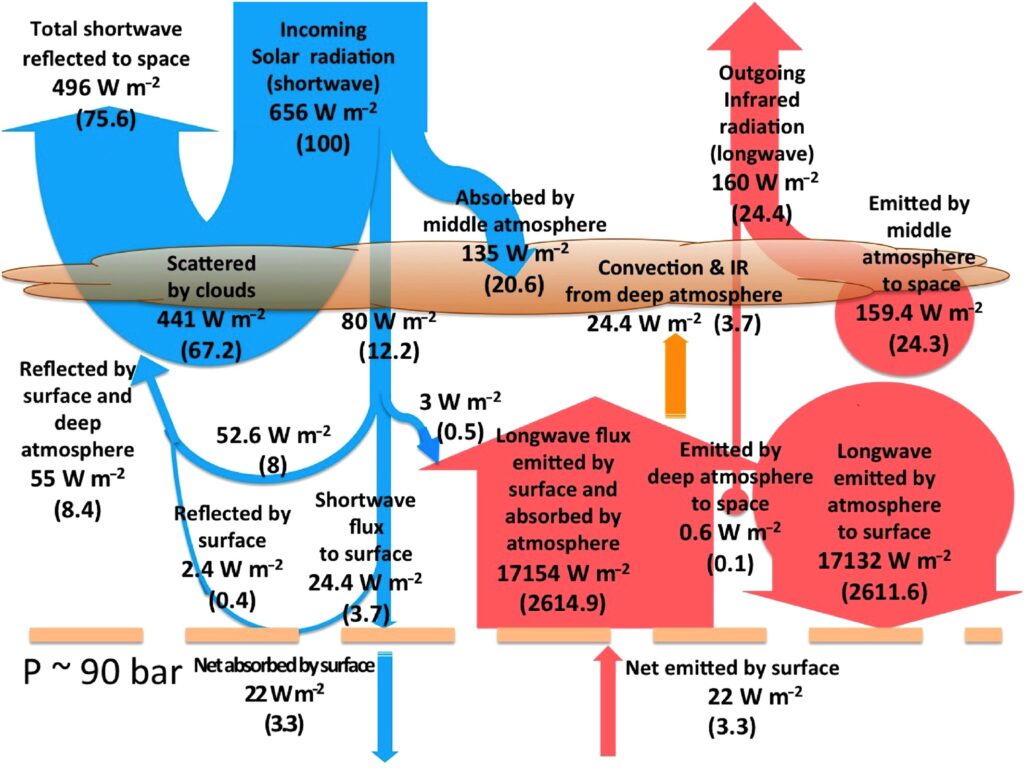
Ceux qui nient l’effet de serre expliquent cette température de surface très élevée par la pression atmosphérique : en comprimant un gaz, on l’échauffe. Oui, mais la surface devrait avoir un rayonnement infrarouge très intense. D’après la loi de Stefan-Boltmann, le flux au sol est de 16 382 W/m² (mais il est estimé à 17 154 W/m² par une étude de 2015). Puisque le sommet de l’atmosphère ne reçoit en moyenne que 650 W/m² du Soleil, Vénus devrait très vite se refroidir ! En réalité, seuls 160 W/m² quittent la planète. Vue de l’extérieur, elle apparaît plus froide que la Terre. Les infrarouges émis par le sol sont donc presque tous absorbés par l’atmosphère et Vénus est incapable de se refroidir.
**************************************************************************************
On trouvera une présentation approfondie de l’effet de serre radiatif dans le chapitre 3 du livre Physique et enjeux de société, écrit par Guillaume Blanc et Camille Noûs et publié en 2023 par l’Université Paris Cité. Il est en libre accès.
Quelques études scientifiques qui parlent du rétro-rayonnement ou flux descendant ondes longues si l’on ne veut pas présumer de son origine :
Rolf Philipona et al., Radiative forcing – measured at Earth’s surface – corroborate the increasing greenhouse effect, Geophysical Research Letters, 06 February 2004 [1].
Wang Kaicun & Liang Shunlin, Global atmospheric downward longwave radiation over land surface under all-sky conditions from 1973 to 2008, Journal of Geophysical Resarch Atmospheres, 011 October 2009 [2].
Graeme L. Stephens et al., The Global Character of the Flux of Downward Longwave Radiation, Journal of Climate, 01 April 2012 [3].
Daniel R. Feldman et al., Observational determination of surface radiative forcing by CO2 from 2000 to 2010, Nature 519, 339–343, 25 February 2015 [4].














Leave a Reply
Vous devez vous connecter pour publier un commentaire.